5 نظریه ریاضی که در طراحی محصول به کمکت میاد
متن به بررسی ارتباط میان ریاضیات و طراحی محصول میپردازد و بهویژه بر نقش فیثاغورث در کشف اصول زیبایی و هارمونی در طبیعت تأکید میکند. ریاضیات، با ارائه نظریاتی همچون تناسب طلایی و دنباله فیبوناچی، به طراحان کمک میکند تا طراحیهایی متناسب و جذاب خلق کنند. همچنین، این علم میتواند در مدلسازی هندسی، بهینهسازی منابع و تجزیهوتحلیل رفتار کاربران نقش مهمی ایفا کند. در نهایت، متن نشان میدهد که چگونه طبیعت و ریاضیات میتوانند در کنار هم، طرحهایی شگفتانگیز و کاربردی ایجاد کنند.
آیا تابهحال به وجه اشتراک چهرهی خود با تخم مرغ، یا وجه شباهت آفتابپرست با آناناس فکر کردهاید؟ جهان هستی جای باشکوه و بینهایت پیچیدهای است که در آن میتوان بین عناصر بهظاهر نامربوط، رابطهای پیدا کرد. تکرار بیشمار الگوهای مشابه در طبیعت به شکلگیری سناریوهای مبهوتکنندهای انجامیده است که به کمک ریاضی بهراحتی قابل توضیح هستند. به قول آرتور بنجامین، ریاضیدان معروف آمریکایی، افراد اغلب به سه دلیل ریاضی یاد میگیرند: برای انجام محاسبات، برای به کار بردن آن در حوزههای مختلف و برای الهام گرفتن از آن.

اینجاست که پای فیثاغورث به ماجرا باز میشه! فیثاغورث فقط یه ریاضیدان نبود؛ اون به دنبال کشف قوانین زیبایی در طبیعت و هنر بود. “تناسبات طلایی” و “هارمونی اعداد” نظریاتی هستند که توی طراحی به کمک ما میان تا تعادل و زیبایی ایجاد کنیم.
بیشتر بخوانید: آشنایی با فیثاغورس
فیثاغورس عموماً به عنوان کاشف قضیه فیثاغورس شناخته میشود، اما نقش او در ریاضیات بسی ژرفتر و برجسته تر است.
البته ریاضیات بسیار پیش تر از فیثاغورس نیز وجود داشته و زمان واحدی را نمیتوان به عنوان آغاز ریاضی ذکر کرد؛ و نقش فیثاغورس تبیین اصول ریاضیات بود.
در دیدگاه فیثاغورس تمام رویدادها تحت تاثیر اصولی کلی رخ می دهند. یک اصل می تواند در شکل گیری یک اثر هنری مطرح گردد اگر نظم موجود در قواعد ریاضی را در نظر داشته باشد. حساب، هندسه، ستاره شناسی و موسیقی، علوم چهارگانه ای هستند که کاملا برمبنای قواعد کلی فوق الذکر شکل گرفته اند. فیثاغورس متقاعد شده بود که هارمونی و تمام موضوعات و اصول موجود در جهان هستی می تواند از طریق اعداد و قواعد ریاضی به خوبی درک شود. او کشف کرد که فاصله موجود میان نت های موسیقی ارتباطات ساده ای را بر اساس تقسیمات تارها و تعداد نوسانات شکل می دهد. بر اساس نظریه فیثاغورس، تتراکتیس: اعداد ۱ تا ۴ (۴ المان، ۴ نقطه اصلی) شالوده و اساس این ارتباطات را تشکیل می دهد. ایده تناسبات هارمونیک، اصلی کلی برای تمام علوم نظری و کاربردی است.
استفاده از ریاضی در طراحی
ریاضیات و طراحی محصول شاید در نگاه اول دو دنیای کاملاً متفاوت به نظر برسند، اما واقعیت این است که ریاضیات میتواند پایه و اساس ایجاد طراحیهای زیبا، کاربردی و بهینه باشد. در ادامه توضیح میدهم که چطور نظریات ریاضی میتوانند به طراحی محصول کمک کنند:تصور کن که داری یه محصول جدید طراحی میکنی. شاید یه صندلی، یه اپلیکیشن یا حتی یه بستهبندی برای یه برند معروف. سوال اینجاست: چطور میتونی طراحیای داشته باشی که هم چشمنواز باشه و هم به دل بشینه؟در ادامه بررسی خواهیم کردچگونه طبیعت و ریاضیات دست در دست هم میدهند تا طرحهایی شگفتانگیز و کاربردی خلق کنند.
بیشتر بخوانید:چگونه ریاضی در طراحی به طراحان کمک میکند:
1. تناسبات و هارمونی در طراحی
ریاضیات به ما کمک میکند تا طراحیهایی متناسب و متعادل ایجاد کنیم. نظریاتی مثل تناسب طلایی (Golden Ratio) و دنباله فیبوناچی راههایی برای دستیابی به زیبایی طبیعی ارائه میدهند. محصولاتی که بر اساس این اصول طراحی میشوند، ناخودآگاه حس جذابیت و هارمونی بیشتری القا میکنند.
مثالها:
- طراحی لوگوها و رابط کاربری بر اساس تناسبات طلایی.\n
- استفاده از دنباله فیبوناچی برای تعیین اندازه و چیدمان عناصر در طراحی وبسایتها و اپلیکیشنها.
2. مدلسازی هندسی و ساختاری
نظریات هندسی مثل استفاده از اشکال ابتدایی (دایره، مربع، مثلث) و شبکهبندی در طراحی، پایههایی برای خلق محصولاتی مستحکم و کاربردی ایجاد میکنند. ریاضیات در اینجا به عنوان ابزاری برای سادهسازی پیچیدگیها و یافتن بهترین فرم و ساختار عمل میکند.
مثالها:
- طراحی خودروها و هواپیماها که از آیرودینامیک و ریاضیات پیچیده برای بهینهسازی عملکرد بهره میبرند.
- استفاده از الگوهای پارامتریک در معماری و مبلمان برای خلق طرحهای مدرن و پیچیده.
3. بهینهسازی منابع و تولید
ریاضیات کمک میکند که طراحیها بهینهتر باشند، یعنی از کمترین مقدار مواد و منابع، بیشترین بهرهوری به دست آید. این کار با کمک مدلسازی ریاضی و الگوریتمهای بهینهسازی ممکن میشود.
مثالها:
- استفاده از الگوریتمهای گرافیکی در طراحی سهبعدی برای کاهش اتلاف مواد در پرینت سهبعدی.
- طراحی بستهبندیهایی که با کمترین مقدار مواد، مقاومتر و جذابتر باشند.
4. تجزیهوتحلیل رفتار کاربران
ریاضیات پشت طراحی فقط به فرم و شکل محدود نمیشود. با کمک تحلیل دادهها، میتوان رفتار کاربران را بررسی کرد و طراحیها را دقیقاً مطابق با نیازها و خواستههای آنها بهبود داد.
مثالها:
- استفاده از تحلیل آماری برای فهم الگوهای استفاده کاربران از یک محصول.
- بکارگیری هوش مصنوعی و الگوریتمهای یادگیری ماشین برای ایجاد رابطهای کاربری شخصیسازیشده.
5. ایجاد ریتم و حرکت در طراحی
در طراحی گرافیکی و صنعتی، ریاضیات میتواند ریتم و الگوهای حرکتی را تعریف کند که چشم را در سراسر محصول هدایت کنند. استفاده از فرکتالها و الگوهای ریاضیاتی مثل تقارنها به طراح کمک میکند تا محصولاتی متوازن و جذاب خلق کند.
مثالها:
- استفاده از فرکتالها در طراحی پارچهها یا گرافیک دیجیتال.\n
- طراحی محیطهای بصری در فیلمها و بازیهای ویدیویی بر اساس الگوهای هندسی ریاضی.
6. نوآوری در ساختارهای غیرمتعارف
یکی از ویژگیهای جالب نظریات ریاضی، این است که میتوانند ما را به سمت شکست قوانین طراحی سنتی هدایت کنند. هندسه غیر اقلیدسی و الگوهای پیچیده ریاضی میتوانند محصولاتی منحصربهفرد خلق کنند.
مثالها:
- طراحی مبلمان یا معماری که از مدلهای پارامتریک و الگوهای پیشرفته ریاضی استفاده میکنند.
- محصولات دیجیتالی که با استفاده از دادههای کاربران به طور پویا تغییر میکنند.
1. فراکتالها: زبان طبیعت در طراحی
فراکتالها ساختارهایی هستند که الگوهای مشابهی در مقیاسهای متفاوت دارند. از شاخههای درختان گرفته تا شکلگیری رعدوبرق و حتی گلکلم رومانسکو، طبیعت پر از این الگوهای جذاب است. فراکتالها نه تنها زیبا هستند، بلکه مفید هم هستند؛ زیرا به ما امکان میدهند ساختارهایی پیچیده و کارآمد ایجاد کنیم.

درباره فراکتلها بیشتر بخوانید…
فراکتال یا بَرخال (Fractal)، ساختاری هندسی است که با بزرگ کردن هر بخش از این ساختار به نسبت معین، همان ساختار نخستین به دست آید. به گفتاری دیگر فراکتال ساختاری است که هر بخش از آن با کلاش همانند است. فراکتال از دور و نزدیک یکسان دیده میشود. به این ویژگی خودهمانندی گویند. فراکتالها یکی از ابزارهای مهم در گرافیک رایانهای هستند و میتوان استفادههای بسیاری از آنها کرد
فرکتال fractal از واژه لاتین fractus یا fractum به معنی شکسته گرفت شدهاست که بیانگر یکی از شناسههای اصلی آن یعنی -بخششدنی- است. فرهنگستان زبان فارسی واژه برخال را تصویب کرده و همچنین برای واژه فرکتالی واژه برخالی را تصویب کردهاست که از واژه برخ به معنی بخش و قسمت و پسوند -ال (مانند چنگال) تشکیل شدهاست و با واژه فراکتال هممعنی است.
رشته کوهها، پشتههای ابر، مسیر رودخانهها و خطوط ساحلی نیز همگی مثالهایی از یک ساختمان خود متشابه هستند. فراکتال شکل هندسی پیچیدهاست که دارای جزئیات مشابه در ساختار خود در مقیاسهای متفاوت میباشد و بی نظمی در آن از دور و نزدیک به یک اندازه است.
جسم فراکتالی از دور و نزدیک یکسان دیده میشود؛ مثلاً وقتی به یک کوه نگاه میکنیم شکلی شبیه به یک مخروط میبینیم که روی آن مخروطهای کوچکتر و بی نظمی دیده میشود ولی وقتی نزدیک میشویم همین مخروطهای کوچک شبیه کوه هستند یا شاخههای یک درخت شبیه خود درخت هستند. البته در طبیعت نمونههای اجسام فراکتال فراوان است مثلاً ابرها -رودها -سرخسها و حتی گل کلم از اجسام فراکتال است؛ و اگر به ساختههای دست بشر هم نگاه کنیم تراشههای سیلیکان یا مثلث سرپینسکی نیز فراکتال هستند؛ و در معماری همیشه نباید نیاز بشر را هندسه اقلیدسی تأمین کند. گسترش شهرها نمونه آشکاری از فراکتال است.
ویژگیهای فراکتالها:
- تکرار در مقیاسهای کوچکتر: هر بخش از یک فراکتال شبیه به کل آن است.
- کارایی در فضا: از فراکتالها برای طراحیهایی استفاده میشود که نیاز به بهرهوری بالا در فضای محدود دارند.
- زیبایی طبیعی: طرحهای فراکتال حس طبیعی و آشنا به بیننده القا میکنند.

مثالهای کاربردی:
- معماری: استفاده از فراکتالها در طراحی نماهای ساختمان، مانند نمای “موزه هنر اسلامی” در دوحه.
- محصولات دیجیتال: طراحی الگوهای پسزمینه برای وبسایتها و اپلیکیشنها.
- صنایع مد: الگوهای پارچههایی که با استفاده از فراکتالها طراحی شدهاند، مانند طرحهای برندهای لوکس.
2. الگوهای مویر: هماهنگی در پیچیدگی

الگوی مویر (Moire Patterns) زمانی به وجود میآید که دو شبکه با فاصله یا زاویه کمی متفاوت روی یکدیگر قرار بگیرند. این الگوها که شامل شکلهایی موجدار یا حلقوی هستند، در عین پیچیدگی، جذابیت و هماهنگی چشمنوازی ایجاد میکنند.
درباره الگوهای مویر بیشتر بخوانید…
اصطلاح الگوی moiré از کلمه فرانسوی “آب داده شده” گرفته شده است زیرا این الگوها اغلب ما را به یاد امواج پاشش ایجاد شده هنگام شکافتن آب می اندازند.
یک الگوی تداخلی ناشی از داشتن دو شبکه مشبک (روکششده در یک زاویه) یا دو شبکه مشبک با فاصله نزدیک (فقط از هم جدا شدهاند). در کارت گرافیک استفاده می شود چاپ و سایر صنایع برای ایجاد تصاویر.
وقتی دو مجموعه از خطوط موازی روی هم قرار می گیرند – اینها الگوهای موآر هستند. فاصله هر جفت خطوط بیشتر از جفت بعدی است. اگر مجموعهای از پارههای خط را بین هر دو نوع خط اضافه کنید، یک الگوی باند روشن تا تیره در چشم ظاهر میشود. عرض نوارها مطابق با فاصله خطوط و همپوشانی دو خط در زوایای مختلف است.
But instead of these, we use moiré patterns for measuring the line spacings. The line separation در اندازه گیری می شود قوانین و مقررات از عرض این نوارها.
راه دیگری که الگوهای موآر می توانند مفید باشند، ایجاد تصاویری چشم نواز است. با تغییر فاصله خطوط و زوایای همپوشانی خطوط می توان به الگوهای مختلف دست یافت.
کاربردهای الگوهای مویر:

- طراحی صنعتی: در طراحی کاورها و بدنههای محصولات الکترونیکی، مثل گوشیهای هوشمند.
- گرافیک متحرک: استفاده از این الگوها برای ایجاد جلوههای بصری در انیمیشنها و ویدئوها.
- هنرهای معاصر: خلق آثار هنری تعاملی که با حرکت مخاطب تغییر میکنند.
3. نظریه تناسب طلایی (Golden Ratio)
تناسب طلایی (Golden Ratio) عددی برابر با تقریبی 1.618 است که به شکل خاصی در طبیعت، هنر، و طراحی دیده میشود. این نسبت زمانی حاصل میشود که نسبت بخش کوچکتر به بخش بزرگتر برابر با نسبت بخش بزرگتر به کل باشد. این اصل از زمان یونان باستان برای ایجاد تعادل و زیبایی استفاده شده است.ایجاد نسبت طلایی عبارت است از تقسیم پاره خط به دو قسمت به طوری که نسبت طول قطعه بزرگ تر به طول تمام پاره خط، مساوی با طول قطعه کوچک تر به قطعه بزرگ تر باشد.
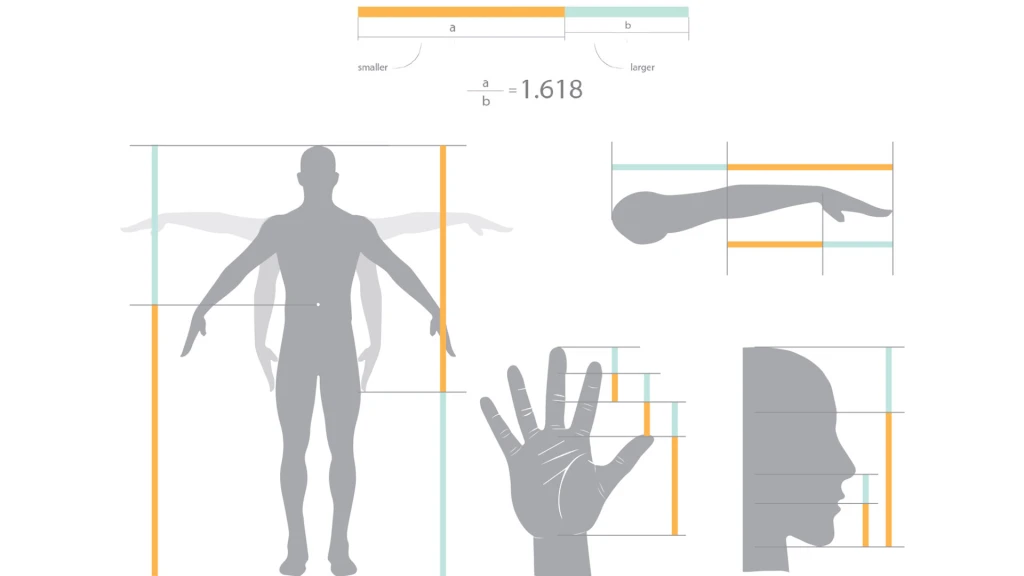

لئوناردو داوینچی در ترسیم نقاشی معروف خود از بدن انسان از نسبت طلایی بهره گرفته است. به عنوان مثال نقاطی از بدن که دارای نسبت طلایی هستند:
- نسبت قد انسان به فاصله ناف تا پاشنه پا.
- نسبت فاصله نوک انگشتان تا آرنج به فاصله مچ تا آرنج.
- نسبت فاصله شانه تا بالای سر به اندازه سر.
- نسبت فاصله ناف تا بالای سر به فاصله شانه تا بالای سر.
- نسبت فاصله ناف تا زانو به فاصله زانو تا پاشنه پا.
لیست آثار هنری طراحی شده با توجه به نسبت طلائی:
http://en.wikipedia.org/wiki/List_of_works_designed_with_golden_ratio
روابط ریاضی حاکم بر عدد طلائی:
http://www.mcs.surrey.ac.uk/Personal/R.Knott/Fibonacci/phi.html
4.ماتریسها (Matrix)
یکی از ابزارهای پرکاربرد ریاضی ، ماتریسها هستند. ماتریسها به ما کمک میکنند که دادهها را ساختاربندی کنیم، گزینههای مختلف را مقایسه کنیم و تصمیمهایی آگاهانهتر بگیریم.
در سادهترین شکل، ماتریسها جدولهایی هستند که اطلاعات را به صورت مرتب سازماندهی میکنند. در طراحی، ماتریسها میتوانند برای:
- شناسایی نقاط قوت و ضعف ایدهها.
- مقایسه گزینههای طراحی.
- اولویتبندی ویژگیها.
ماتریس ها رو در مطلبی جداگانه و مفصل تر پرداخت کردهایم؛ از اینجا بخوانید.

5. نظریه هارمونی اعداد
هارمونی اعداد، به دنبال ترکیب اعداد و نسبتهایی است که حس تعادل و نظم را منتقل میکنند. یکی از نمونههای معروف آن دنباله فیبوناچی است؛ دنبالهای که هر عدد مجموع دو عدد قبلی خود است (1، 1، 2، 3، 5، 8 و …). این دنباله در طبیعت و طراحی کاربردهای فراوانی دارد.
- از دید محاسباتی، درک این دنباله بسیار آسان است: ۱ به اضافهی ۱ میشود ۲؛ ۲ به اضافهی ۱ میشود ۳؛ ۳ به اضافهی ۲ میشود ۵ و الی آخر.
- از دید کاربردی هم اعداد فیبوناچی بهوفور در طبیعت یافت میشوند. تعداد گلبرگهای گل، شکل تخممرغ و آناناس، پیچش دم آفتابپرست یا چینش مارپیچی تخمهای گل آفتابگردان از دنبالهی فیبوناچی پیروی میکنند.
چرا نظریات ریاضی در طراحی مهم هستن؟
الگوهای ریاضی به طراحان کمک میکنند تا:
- هماهنگی، تناسب و زیبایی بصری: ایجاد تعادلی که ناخودآگاه مخاطب را جذب میکند.طراحیهایی که بر اساس اصول هندسی ساخته میشن، ناخودآگاه حس خوشایندتری به مخاطب میدن.
- کارایی و عملکرد: بهرهوری در فضا، زمان و مواد مصرفی.
- نوآوری: ایجاد طرحهای جدیدی که با تکنیکهای دستی امکانپذیر نبودند.
- هدایت چشم: استفاده از خطوط و زاویههای درست، باعث میشه کاربر بهطور طبیعی به مهمترین بخش طراحی تو جلب شه.
- افزایش اعتماد: یه طراحی منظم و متقارن ناخودآگاه حس اعتماد بیشتری رو در مخاطب ایجاد میکنه.
کاربرد در صنایع مختلف:
- طراحی محصول: از طراحی مبلمان گرفته تا گجتهای هوشمند، رعایت این اصول میتونه به ایجاد محصولاتی باکیفیت و محبوب منجر بشه.
- معماری: طراحی ساختمانهایی که از تناسبات طلایی بهره میبرند، اغلب چشمنوازتر و حس استحکام بیشتری القا میکنند.
- تبلیغات و برندینگ: طراحی لوگوها و پوسترهایی که از این اصول پیروی میکنن، معمولاً تأثیرگذاری بیشتری دارن.
- تجربه کاربری (UX): چینش دقیق عناصر و رعایت تعادل در طراحی رابط کاربری، تجربهای لذتبخشتر برای کاربر فراهم میکنه.
مثالهایی از طبیعت و هنر:
- طبیعت: ساختار گلها و حتی نحوه قرارگیری دانههای آفتابگردان از اصول تناسبات طلایی پیروی میکنند. پوسته حلزونها یا شکل کهکشانها نیز نمونههایی دیگر از این تناسب در طبیعت هستند.
- هنر و معماری: نمای پارتنون در یونان باستان یکی از معروفترین نمونههای استفاده از تناسب طلایی است. نقاشی مونالیزا اثر داوینچی نیز این اصول را بهخوبی به کار گرفته است.
- صنعت مد و زیبایی: طراحی لباسهایی که از خطوط و تناسبات طلایی استفاده میکنن، اغلب چشمنوازتر و جذابتر به نظر میرسن.
- محصولات دیجیتال: در طراحی اپلیکیشنها و وبسایتها، شبکهبندی و چینش عناصر با این اصول، تجربه کاربری بهتری رو فراهم میکنه.
استفاده از نظریات ریاضی در طراحی
ابزارها و نرمافزارها برای خلق الگوهای ریاضی:
- Grasshopper: پلاگینی برای Rhino که امکان طراحی پارامتریک و فراکتال را فراهم میکند.
- Processing: ابزاری برای خلق الگوهای مور و طرحهای تعاملی.
- Adobe Illustrator: برای طراحی الگوهای دقیق با استفاده از شبکههای تکرارشونده.
پایان ماجرا: قدرت منطق در زیبایی
ریاضیات فقط یک ابزار نیست؛ بلکه زبان جهانی برای فهم زیبایی، نظم و کارایی است. با استفاده از نظریات ریاضی در طراحی محصول، میتوان محصولاتی خلق کرد که نه تنها زیبا و کاربردی هستند، بلکه بهینه، هدفمند و حتی الهامبخشاند. از طبیعت گرفته تا هنر و فناوری، ریاضیات همواره پایه و اساس طراحیهای ماندگار بوده و خواهد بود.از فراکتالها تا الگوهای مور، ریاضیات در طراحی راهی برای ایجاد هارمونی، جذابیت و کارایی است. این الگوها به ما یادآوری میکنند که زیبایی و منطق همیشه میتوانند با هم همکاری کنند و محصولات و طرحهایی خلق کنند که هم چشمنواز و هم کاربردی باشند.
نسبت اعداد متوالی فیبوناچی (۲/۱، ۳/۲، ۵/۳ و …) به مقدار نسبت طلایی نزدیک است. در واقع، هرچه اعداد فیبوناچی بزرگتر باشند، یا به عبارت دیگر هرچه در این دنباله به سمت بینهایت حرکت کنیم، نسبت آنها به ۱٫۶۱۸ یا همان عدد فی نزدیکتر میشود. از آنجایی که نسبت طلایی بهوفور در طبیعت یافت میشود، به آن «نسبت الهی» نیز میگویند.
وقتی اصول ریاضی رو در طراحیهات به کار ببری، نه تنها محصولاتی زیباتر خلق میکنی، بلکه این زیبایی با منطق و هدف همراه خواهد بود. این یعنی خلق آثاری با اصالت، غنی و انسانمحور که میتونن در هر صنعتی بدرخشن.
پس دفعه بعد که پشت میز طراحی نشستی، یادت باشه که ریاضی میتونه بهترین دوستت باشه!